La NASA coloca en órbita circular un satélite artificial de 300 kg de masa, de forma que un observador terrestre, convenientemente situado, podría verlo inmóvil en el firmamento. Este tipo de satélite se denomina geoestacionario o geosincrónico, y se utiliza principalmente en comunicaciones.
-
Calcula el radio de la órbita y su altura respecto a la superficie terrestre.
-
Determina la energía mecánica del satélite en su órbita.
Datos: Constante gravitación Universal, G = 6,67·10-11 U.S.I., masa de Tierra, M=5,97·1024 kg
SOLUCIÓN
- Que el satélite sea geoestacionario nos lleva a que el periodo de su órbita en torno a la Tierra sea de 24 horas, es decir, 86400 s
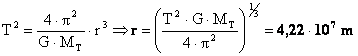
Así pues, el problema se reduce a obtener el radio de la órbita conocido el periodo, que podemos resolver haciendo uso de la 3ª ley de Kepler en combinación con la L.G.U. de Newton que nos permite decir:
Y, por lo tanto su altura sobre la superficie será:
h = r - RT = 3,58·107 m
-
La energía de un satélite en órbita es:
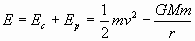
Pero como la órbita es circular:
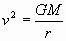
Por lo que la energía de una órbita circular se puede expresar como:
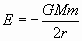
Sustituyendo r por el valor obtenido, resulta:
E = -1,41·109 J
|