|
Una bolita de masa m =
0,5 kg, apoyada sobre una superficie horizontal sin rozamiento, está unida a una
pared
mediante un muelle de masa despreciable y constante recuperadora k = 50
N/m. Se desplaza m hacia la derecha 2 cm, y se suelta con velocidad nula
de forma que la bolita comienza a oscilar armónicamente en torno a su posición
de equilibrio, O.
-
Determine la frecuencia ω y el periodo T de
la oscilación. Escriba la ecuación del movimiento armónico de la bolita.
-
Represente gráficamente la velocidad de m en
función del tiempo.
-
Calcule la energía mecánica de m.
SOLUCIÓN
-
Recordando la relación entre frecuencia angular (ω) y
constante elástica (k): ω² = (k/m), sustituyendo los datos del enunciado, se
obtiene:
ω
= 10 rad/s
Expresando la frecuencia angular en función del periodo
( ω
= 2·π /T), despejando el periodo:
T = 0,2·π s
Para expresar la ecuación del movimiento armónico de la
bolita, tomamos como origen de tiempos el momento en el que se suelta la
bolita (extremo derecho del dibujo) y la ecuación corresponde a la forma: x
= A · cos ( ω·t)
x (t) = 0,02 · cos 10 t (x en m y t en s)
-
La expresión de la
velocidad de la bolita en función del tiempo se obtiene derivando la
ecuación de la elongación respecto a t:
v (t) = 0,02 · 10 · (- sen 10 t) = - 0,2 · sen 10 t
(v en m/s y t en s)
Representando gráficamente la ecuación anterior
-
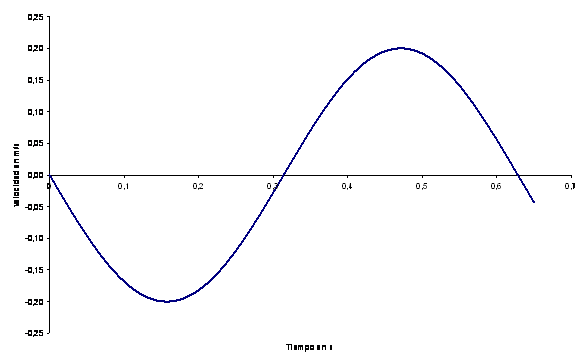
Una forma de calcular la energía mecánica es utilizar la
expresión de la energía potencial elástica máxima (energía mecánica de la
bolita en cualquiera de ambos extremos, siendo su energía cinética en esos
puntos igual a 0): EM = ½· k· A². Sustituyendo los datos del
enunciado:
EM = E P máxima = ½ · 50 · 0,02²
= 0,01 J
También podríamos calcularla a partir de la velocidad
máxima que tiene la bolita cuando pasa por el punto de equilibrio (energía
potencial elástica igual a 0):
EM = E cinética máxima =½ ·
m · v²max = ½ · 0,5 · 0,2² = 0,01 J
Siendo vmax = ±A ·
ω
= ± 0,02 · 10 = 0,2
m/s
Como la energía mecánica es constante (sólo actúa la
fuerza elástica que es conservativa), en cualesquiera otros puntos del
movimiento, a excepción de los citados anteriormente, los valores de la
energía cinética y potencial elástica serán distintos de cero y la suma de
ambas energías será de 0,01 J.
|
