Septiembre 99-00, Opción A

Una sonda de exploración, de masa 500 kg., describe una órbita circular en torno a Marte. Sabiendo que el radio de dicha órbita es R = 3,50·10⁶ m, que la masa de Marte es M = 6,42·10²³ kg. y que G = 6,67·10^-11 N·m²/kg², calcula:

1. La velocidad orbital de la sonda y su momento angular respecto de Marte.

2. Las energías cinética, potencial y mecánica de la sonda.

1. Velocidad orbital de la sonda:

Para una órbita circular, la fuerza de atracción que ejerce Marte sobre la sonda es perpendicular a su velocidad, por lo tanto le comunica una aceleración centrípeta. De aquí se puede calcular la velocidad orbital:

F_G = m·a_c

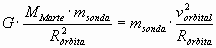
Simplificando y despejando la velocidad orbital, se llega a:

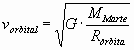
Sustituyendo los datos del enunciado:

v_orbital = 3498 m/s

Momento angular de la sonda respecto a Marte:

Considerando la sonda como una masa puntual, el módulo del momento angular se obtiene:

L = R_órbita·m_sonda·v_orbital·sen 90º

Sustituyendo los datos del enunciado y el calculado par ala velocidad orbital, se obtiene:

L = 6,12·10¹² kg·m² /sg

 

2. Energía cinética de la sonda;

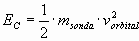
Sustituyendo los datos del enunciado, se obtiene:

E_C = 3,06·10⁹ J

Energía potencial de la sonda;

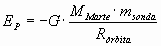
Sustituyendo los datos del enunciado, se obtiene:

E_P = -6,12·10⁹ J

Energía mecánica de la sonda;

E_M = E_C + E_P

E_M = -3,06·10⁹ J

Se comprueba que al ser una órbita circular, la energía mecánica es la mitad de la energía potencial.