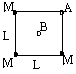Septiembre 98-99, Opción B

Tres partículas iguales de masa M están fijas en los vértices de un cuadrado de lado L.

1. Determina el potencial gravitatorio en los puntos A y B, vértice vacante y centro del cuadrado, respectivamente.

2. Si situamos una cuarta partícula en el punto A y la soltamos con velocidad inicial nula, se moverá hacia B. ¿Por qué?. Determina la velocidad de esta partícula cuando pase por B.

Supón conocida la constante de gravitación universal.

1. El potencial gravitatorio que crea una partícula de masa M en un punto P situado a una distancia R de la partícula es:

Si son varias las masas que se encuentran en las proximidades del punto P, el potencial total corresponderá a la suma de los potenciales de cada una de las masas.

Potencial en el punto A:

Llamando 1, 2 y 3 los vértices del cuadrado donde se encuentran las masas M en el sentido horario, (comenzando en el vértice A) los potenciales que crean las masas M de los puntos 1 y 3 son iguales al ser la misma la distancia al punto. En el caso de la masa en el vértice 2, la distancia corresponde a la diagonal del cuadrado de lado L.

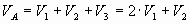
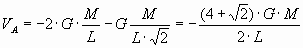
y

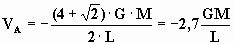
Potencial en el punto B:

En este caso los potenciales de las tres partículas en el punto B son los mismos ya que son iguales las distancias al punto central del cuadrado. Así:

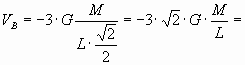
y

2. Una partícula de masa m situada en un punto de un campo gravitatorio tiende a moverse desde los puntos de potenciales elevados hacia los puntos de potenciales bajos. Como el potencial en el punto A es mayor que en el punto B, la partícula abandonada en el punto A se moverá hacia B por la acción del campo.

Como la fuerza gravitatoria es una fuerza conservativa, la energía mecánica se conserva. Aplicando el principio de conservación de energía:

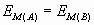
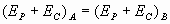
Como la velocidad inicial de la partícula es nula y sabiendo que la energía potencial de la partícula en un punto corresponde al producto de la masa por el potencial en ese punto, se puede escribir: