Un satélite artificial de la Tierra recorre una órbita circular de radio r = 5RT. Si supones que el único astro del Universo es la Tierra calcula:
-
La velocidad orbital del satélite.
-
Se sabe que la energía que tienen que suministrar los cohetes de a bordo para que el satélite se libere de la atracción terrestre y alcance el infinito vale 1,25ˇ1010 J. Calcula la masa del satélite.
Datos: Aceleración de la gravedad en la superficie de la Tierra (go) = 9,8 m/s˛
Radio de la Tierra: 6,37ˇ106 m.
SOLUCIÓN
-
La velocidad orbital de un satélite que describe una órbita circular se puede deducir a partir de que la fuerza de atracción gravitatoria en esa órbita es perpendicular a la velocidad y, por lo tanto, comunica al satélite una aceleración centrípeta.
FG = mˇac
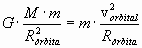
Despejando la velocidad:
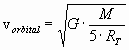 (1) (1)
Teniendo en cuenta los datos del enunciado, debe expresarse el producto (GˇM) en función de la aceleración de la gravedad y del radio de al Tierra.
Partiendo de la expresión de la aceleración de la gravedad:
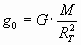
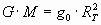 (2) (2)
Sustituyendo este resultado en la ecuación (1):
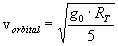
vorbital = 3533 m/s
-
La energía (D
E) que tienen que comunicar los cohetes de a bordo corresponde a la diferencia entre la energía mecánica que tendrá el satélite cuando abandone la atracción gravitatoria (EM = 0) y la energía mecánica en la órbita (EM = ˝ EP, ya que se trata de una órbita circular).
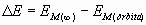
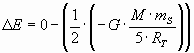
Sustituyendo el producto (GˇM) por la expresión (2)
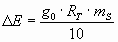
Despejando la masa del satélite y sustituyendo los datos del enunciado, se obtiene:
mS = 2002 kg
|