Septiembre 06-07, Opción B

1. Definir el concepto de fuerza conservativa indicando dos ejemplos reales

2. Justificar la relación entre la fuerza y la energía potencial gravitatoria.

3. La Estación Espacial Internacional (ISS) describe alrededor de la Tierra una órbita prácticamente circular a una altura h = 390 km sobre la superficie terrestre. Calcula su energía cinética y su energía potencial respecto al campo gravitatorio, sabiendo que su masa es de 4,2·10⁵ kg.

G = 6,67·10^-11 N m² kg^-2; M_T = 5,97·10²⁴ kg ¸ R_T = 6,38·10⁶ m

SOLUCIÓN

1. Se pueden dar 3 definiciones de fuerza conservativa, todas equivalentes:

• Una fuerza es conservativa si el trabajo que realiza dicha fuerza al desplazarse el cuerpo sobre el que se aplica desde un punto A hasta otro B es independiente del camino seguido para ir de A a B y solo depende de ambos puntos
• Una fuerza es conservativa si el trabajo que realiza dicha fuerza en una trayectoria cerrada, saliendo y llegando al mismo punto, es nulo
• Una fuerza es conservativa si existe una función que depende del punto, que llamaremos energía potencial, de modo que podemos calcular el trabajo realizado por la fuerza al desplazarse el cuerpo sobre el que se aplica desde un punto A hasta otro B, como la diferencia de los valores de dicha función en esos puntos, cambiada de signo. Es decir:

Las 3 definiciones son equivalentes, como se puede ver casi inmediatamente.

Como ejemplos de fuerzas conservativas citaremos las fuerzas que estudiamos este curso:

• La fuerza gravitatoria
• La fuerza eléctrica
• La fuerza elástica recuperadora de un muelle

2. Según la 3ª definición, al ser la fuerza gravitatoria conservativa debe existir esa energía potencial. Para obtener su expresión debemos calcular el trabajo realizado por la fuerza gravitatoria en un desplazamiento.

Sean dos cuerpos de masas M y m. La fuerza gravitatoria que se ejercen es según la L.G.U.

 

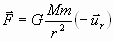
Donde u_r es el vector unitario en la dirección de la línea que une los centros de los dos cuerpos, y el signo – indica que es atractiva.

Si, manteniendo M fija, desplazamos el cuerpo m desde la posición A (determinada por el vector 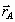) hasta la posición B (determinada por el vector 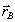) ,el trabajo realizado por la fuerza gravitatoria será:

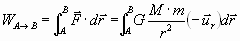
El producto escalar da como resultado –dr (escalar), es decir no el vector desplazamiento infinitesimal sino la variación infinitesimal de la distancia entre ambos cuerpos, con lo que la integral pasa a ser de una sola variable –r– y se puede realizar

Así pues, obtenemos:

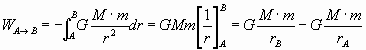
La expresión final se puede interpretar como la variación de una función que depende de r, así que definimos

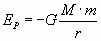
Y, entonces podemos expresar el trabajo como:

W = -E_P(B) + E_P(A) = -ΔE_P

Por tanto el trabajo realizado por la fuerza gravitatoria en una modificación de un sistema lo podemos obtener mediante la variación de la energía potencial gravitatoria del sistema, pero cambiada de signo

3. Según acabamos de ver, la energía potencial será:

Para obtener la energía cinética podemos utilizar el resultado de que, para órbitas circulares, la energía cinética es la mitad de la potencial cambiada de signo