Junio 98-99, Opción B
Atrás Arriba Siguiente

 

  1. Enuncia la tercera ley de Kepler y comprueba que se cumple para órbitas circulares en torno a un planeta esférico de masa M.

  2. Los satélites de comunicaciones geoestacionarios describen órbitas circulares en el plano ecuatorial de la Tierra. El periodo de estas órbitas coincide con el de la rotación de la Tierra (un día), de forma que cada satélite geoestacionario se encuentra siempre sobre el mismo punto del Ecuador. Calcula el radio de esta órbita.

Datos: MT = 6ˇ1024 Kg.; G = 6,67ˇ10-11 Nˇm˛/kg˛

 

SOLUCIÓN

  1. La tercera ley de Kepler se puede enunciar del modo siguiente:

"el cociente entre el cuadrado de los periodos de rotación de los planetas y el cubo de sus distancias medias al Sol se mantiene constante"

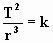
Esta ley también se cumple para cualquier otro sistema formado por un planeta de masa M y uno o varios objetos que orbiten en torno a M. En este caso, el valor de la constante k es distinto.

La comprobación que ese cociente se mantiene constante se puede realizar, para una órbita circular, partiendo de la Ley de gravitación universal de Newton.

La única fuerza que actúa sobre el objeto es la de atracción gravitatoria por parte del planeta y es perpendicular a la velocidad; por lo tanto le comunica una aceleración centrípeta al objeto:

FG = mˇac

Recordando que la aceleración centrípeta corresponde al cociente entre la velocidad al cuadrado y el radio de giro (ac = v2 /r) y, como se trata de una órbita circular, la velocidad se puede calcular por el cociente entre la longitud recorrida en una vuelta completa (2ˇp ˇr) y el tiempo invertido (T), se puede expresar de este modo:

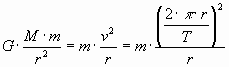
Reorganizando los términos anteriores, se llega a:

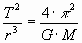
El primer miembro corresponde a la tercera ley de Kepler.

De la igualdad anterior se deduce que la constante "k" de la tercera ley de Kepler es realmente constante ya que depende de la constante de gravitación universal (G) y de la masa del planeta (M), también constante.

 

  1. Para hallar el radio de la órbita geoestacionaria del satélite partimos de la tercera ley de Kepler que, en el sistema Tierra-satélite toma la siguiente forma:

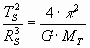
TS representa el periodo y RS el radio de la órbita del satélite geoestacionario.

Despejando el radio RS y sustituyendo los valores dados en el enunciado (1 día = 86400 s), se obtiene:

RS = 42297524 m = 4,23ˇ107 m