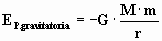Junio 02-03 Opción A

1. Explica el concepto de energía potencial gravitatoria. ¿Qué energía potencial gravitatoria tiene una partícula de masa m situada a una distancia r de otra partícula de masa M?

2. Un planeta esférico sin atmósfera tiene masa M = 1,2.10²³ kg y radio R = 1,3.10⁶ m. Desde su superficie se lanza verticalmente un proyectil que llega a alcanzar una altura máxima h = R/2 antes de volver a caer hacia la superficie. ¿Con qué velocidad inicial se ha lanzado el proyectil? G= 6,7.10^-11 Nm²kg^-2.

1. Energía potencial gravitatoria: Es la energía potencial de una partícula de masa m asociada a la posición que ocupa en un campo gravitatorio creado por otra partícula de masa M.

Como la fuerza de atracción gravitatoria es una fuerza conservativa, el trabajo desarrollado por esa fuerza únicamente depende de la posición inicial y final, pero no depende de la trayectoria seguida.

En estas condiciones, el trabajo desarrollado por la fuerza conservativa lleva asociada una función de energía potencial cambiada de signo, o dicho de otro modo, la variación negativa de la energía potencial gravitatoria viene medida por el trabajo desarrollado por la fuerza de atracción gravitatoria:

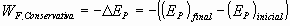
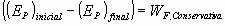
Como lo que en realidad interesa es la variación de la energía potencial, basta con asociar a una posición de referencia inicial el valor de energía potencial igual a 0. Por ejemplo, se asigna el valor de energía potencial igual a cero al punto en el que la fuerza gravitatoria sea cero. Pero se puede tomar cualquier otro punto de referencia.

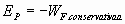
Según este resultado, la energía potencial gravitatoria corresponde al trabajo realizado por la fuerza gravitatoria, cambiado de signo, para trasladar la masa m desde el infinito hasta la distancia r de la masa M.

Energía potencial gravitatoria de una partícula de masa m situada a una distancia r de otra partícula de masa M.

Teniendo en cuenta lo expresado anteriormente, basta calcular el trabajo (cambiado de signo) realizado por la fuerza gravitatoria desde el infinito hasta el punto situado a una distancia r de la masa M.

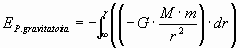
Resolviendo la integral, se obtiene una expresión para la energía potencial gravitatoria de una partícula de masa m situada a una distancia r de otra partícula de mas M

 

2. Como la fuerza que actúa un instante después del lanzamiento es la fuerza de atracción gravitatoria y se trata de una fuerza conservativa, la energía mecánica se mantiene constante. Esto significa que la energía mecánica en el punto inicial (un instante después del lanzamiento) (A) será igual que la energía mecánica en el punto de altura máxima (B).

Luego:

(E_C + E_P)_A = (E_C + E_P)_B

Sustituyendo los datos del enunciado, se llega a:

v₀ = 2026 m/s