-
Enuncia las leyes de Kepler
-
Europa es un satélite de Júpiter que tarda 3,55 días en recorrer su órbita, de 6,71·108 m de radio medio, en torno a dicho planeta. Otro satélite de Júpiter, Ganímedes, tiene un período orbital de 7,15 días. Calcula el radio de Ganímedes y la masa de Júpiter.
Constante de gravitación: G = 6,67·10-11 N·m²/kg²
SOLUCIÓN
-
Primera Ley de Kepler:
"Los planetas se mueven en órbitas elípticas alrededor del Sol, que está situado en uno de sus focos"
Segunda Ley de Kepler:
"La línea imaginaria que une el Sol con el planeta barre áreas iguales en tiempos iguales". Esto significa que los planetas se mueven más deprisa cuanto más cerca están del Sol y más lentos cuanto más lejos.
La ley puede expresarse también diciendo que "la velocidad areolar de los planetas es constante"
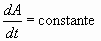
donde A representa el "área barrida" por la línea imaginaria.
Tercera ley de Kepler:
"el cociente entre el cuadrado de los periodos de rotación de los planetas y el cubo de sus distancias medias al Sol se mantiene constante"
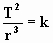
El valor de la constante k depende del sistema que se considere. Tiene distinto valor si se trata del sistema Sol-planetas o del sistema Tierra-satélites o etc.
-
Para calcular el radio medio de la órbita de Ganímedes, se parte de la tercera ley de Kepler:
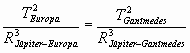
Despejando el radio medio de Ganímedes, se obtiene:
RGanímedes = 1,07·109 m
Para calcular la masa de Júpiter, partimos de la 3ª ley de Kepler, expresando la constante k a partir de la ley de gravitación universal.
Para el caso del sistema Júpiter-Europa, la ley toma la siguiente forma:
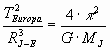
Despejando la masa de Júpiter y sustituyendo los datos del enunciado se obtiene:
MJ = 1,9·1027 kg
|