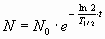Si la atmósfera se hubiese contaminado hoy con un isótopo radiactivo (emisor
γ
; período de semidesintegración 80 años) que se hubiera repartido uniformemente por toda ella,
¿qué fracción de la actividad de hoy les tocaría padecer a tus nietos?. Haz la hipótesis de que tendréis, en promedio, un nieto dentro de 40 años.
El periodo de semidesintegración es el tiempo que debe transcurrir para que la mitad de los núcleos de una muestra radiactiva se hayan desintegrado; o lo que es lo mismo, el tiempo para que la mitad de los núcleos de la muestra no se hayan desintegrado.
Esto significa que han de transcurrir
Ø
80 años para que la actividad de la atmósfera se reduzca a la mitad de la muestra original.
Ø
160 años (2·T1/2) para que la actividad se reduzca a la mitad de la mitad (la cuarta partede la muestra original)
Ø
240 años (2·T1/2) para que la actividad se reduzca a la mitad de la mitad de la mitad (la octava parte de la muestra original)
La relación entre el número de núcleos que permanecen radiactivos y el tiempo transcurrido se puede obtener del modo siguiente:
Llamando N0 al número de núcleos radiactivos en el instante inicial
|
Tiempo transcurrido
|
Núcleos que permanecen sin desintegrar (N) |
|
t = T1/2 |
N0 /2 |
|
t = 2·T1/2 |
N0 /22 |
|
t = 3·T1/2 |
N0 /23 |
En forma general, se puede escribir:
N = N0 / 2n = N0 · 2-n
Donde n representa el número de periodos de semidesintegración transcurridos.
En este caso, el tiempo transcurrido es la mitad de T1/2, luego sustituyendo:
N / N0 = 2- ½ = 0,71
Luego la fracción de la actividad que les tocaría a los nietos sería el 71% de la actividad actual.
El mismo resultado obtendríamos aplicando directamente a ley
de desintegración radiactiva: