Junio 01-02, Opción B

1. ¿Qué es la actividad (o velocidad de desintegración) de una muestra radiactiva?
2. El periodo de semidesintegración del ⁶⁰Co es T = 5,27 años. Calcula la actividad radiactiva de una muestra que inicialmente contiene 10²² átomos de ⁶⁰Co. ¿Cuánto tiempo tarda la actividad de esta muestra en reducirse a la octava parte de la inicial?.

1. La radiactividad es un proceso espontáneo que tiene lugar en el núcleo de los átomos y que puede estudiarse mediante leyes estadísticas. La realidad es que no puede predecirse cuándo se desintegrará un núcleo concreto pero sí se puede determinar la probabilidad de que un núcleo cualquiera se desintegre.

Llamamos actividad de una sustancia radiactiva (A) al número de partículas emitidas por unidad de tiempo, o de otro modo, el número de núcleos que se desintegran por unidad de tiempo.

En un proceso de desintegración radiactiva, el número de núcleos desintegrados (dN), en un tiempo (dt) es proporcional al número de núcleos presentes en un cierto instante y una constante característica de cada sustancia. Por lo tanto, se puede expresar la actividad de una sustancia (o velocidad de desintegración) como:

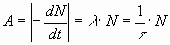
Ø N representa el número de núcleos presentes sin desintegrar

Ø λ corresponde a la constante radiactiva o constante de desintegración, característica de cada isótopo; representa la probabilidad por unidad de tiempo de que se desintegre un núcleo; si su valor es grande, la sustancia se desintegra muy rápidamente, y si es pequeña, el proceso será lento. Se mide en unidades inversas de tiempo.

Ø τ  representa la vida media de un isótopo (corresponde al inverso de la constante radiactiva λ ) y viene a representar un promedio de vida que se espera que tenga un núcleo. Se mide en unidades de tiempo.

Ø El signo – indica que el número de núcleos sin desintegrar va disminuyendo con el tiempo.

Ø La unidad de medida de la actividad en el S.I. es el Bequerel (Bq) que equivale a 1 desintegración por segundo.

2. Hallamos en primer lugar el valor de la constante radiactiva:

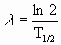
λ= 0,1315 años^-1 = 4,17·10^-9 sg^-1

La actividad de la muestra es:

A₀ = λ· N₀ = 0,1315 · 10²² = 1,315·10²¹ desintegraciones · año^-1 = 4,17·10¹³ Bq

Para calcular el tiempo que debe transcurrir para que la actividad de la muestra se reduzca a la octava parte se puede hacer de forma intuitiva. A partir del instante inicial,

Ø cuando haya transcurrido un tiempo igual a T_1/2, el número de núcleos radiactivos se reduce a la mitad;

Ø cuando haya transcurrido un tiempo igual a 2 T_1/2, el número de núcleos radiactivos se reduce a la mitad de la mitad, la cuarta parte de la muestra inicial

Ø cuando haya transcurrido un tiempo igual a 3 T_1/2, el número de núcleos radiactivos se reduce a la mitad de la mitad de la mitad, la octava parte de la muestra inicial.

Luego el tiempo que debe transcurrir es igual a 3 periodos de semidesintegración

t_1/8 = 3 · T_1/2 = 3 · 5,27 = 15,8 años

A partir de la ley exponencial de desintegración:

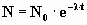
teniendo en cuanta que N = 1/8 de N₀, simplificando y tomando logaritmos neperianos:

1/8 · N₀ = N₀ · e^{- λ ·t}

ln (1/8) = - λ · t_1/8

t_1/8 = 15,8 años