El objeto se sitúa a una distancia ligeramente mayor que la focal del objetivo, para producir una primera imagen real, invertida y mayor del objeto. El ocular se coloca (mediante el mecanismo de enfoque) de manera que la imagen antes descrita caiga a una distancia inferior a la focal del ocular, así la segunda imagen será una imagen virtual, derecha y mayor de la primera.
Como resultado final obtenemos una imagen virtual, bastante mayor e invertida del objeto.
Para la observación por el ojo interesa que la imagen sea virtual y para la comodidad del mismo que se forme en el infinito. Eso hace que la imagen dada por el objetivo deba encontrarse precisamente en el foco del ocular.
El aumento del objetivo, para esta situación en la que la imagen se forma en el foco objeto del ocular (es decir: s’ = L + f’), lo podemos obtener teniendo en cuenta que:
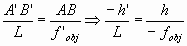
por lo que el aumento lateral del objetivo será:
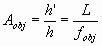
Por otra parte, el aumento comercial del ocular tomado como el de una lupa será:
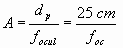
Así pues, el aumento total del microscopio será el producto de ambos aumentos:
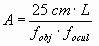
Aplicando la ecuación de las lentes:
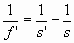
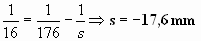
Es decir, a 17,6 mm por delante (a la izquierda) del objetivo. Un poco más lejos del foco objeto