Junio 03-04, Opción A

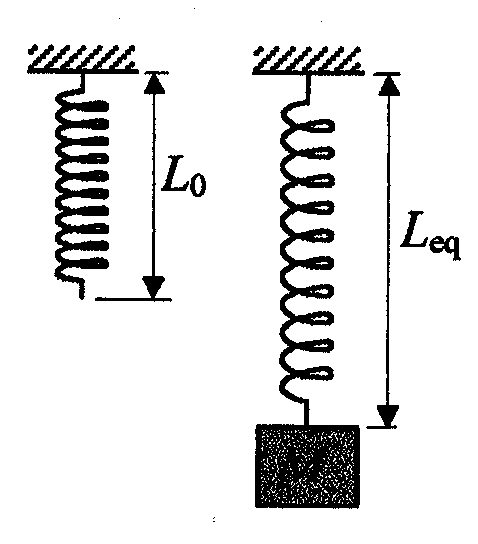
Un muelle de masa despreciable tiene una longitud natural L₀ = 20 cm. Cuando de su extremo inferior se cuelga un cuerpo de masa M = 0,1 kg, la longitud en equilibrio del muelle es L_eq = 30 cm.

1. Calcula la constante recuperadora, k, de este muelle.

Partiendo de la posición de equilibrio anterior, se desplaza M hacia arriba 10 cm, es decir hasta que el muelle tiene su longitud natural. A continuación se suelta M con velocidad inicial nula, de forma que empieza a oscilar armónicamente en dirección vertical.

2. Calcula la longitud máxima del muelle, en el punto más bajo de la oscilación de M.

3. Calcula la amplitud y la frecuencia de la oscilación, y la velocidad de M cuando pasa por su posición de equilibrio

1. En la posición de equilibrio actuarán dos fuerzas opuestas sobre el cuerpo: el peso, hacia abajo, y la fuerza elástica del muelle, hacia arriba. Ambas fuerzas deberán ser iguales, por lo que podemos escribir, aplicando la ley de Hooke a la fuerza realizada por el muelle:

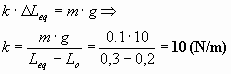
2. En la oscilación armónica del muelle en dirección vertical se conserva la energía mecánica ya que las únicas fuerzas que actúan son la de la gravedad (peso) y la fuerza elástica.

Tomamos como situación inicial cuando el muelle mide su longitud natural (L₀) y como situación final, el punto más bajo de oscilación de la masa M (L₀ +y).

Como origen de energía potencial gravitatoria tomamos el punto más bajo de la oscilación, al que asignamos un valor 0.

Aplicando el principio de conservación de la energía para ambas posiciones:

(E_cinética + E_{potencial gravitatoria} + E_{Potencial elástica})_inicial =

(E_cinética + E_{potencial gravitatoria} + E_{Potencial elástica})_final

0 + m·g·y + 0 = 0 + 0 + ½·k·y²

Simplificando: m·g = ½·k·y

Si tenemos en cuenta lo dicho en el apartado a)

m·g = k·(L_equilibrio – L₀)

Igualando

½·k·y = k·(L_equilibrio – L₀)

Despejando y, se obtiene:

y = 2·(L_equilibrio – L₀)

Así pues, la longitud máxima del muelle será:

Longitud máxima del muelle = L₀ + 2·(L_equilibrio – L₀)

Llamando al paréntesis anterior A (amplitud del movimiento oscilatorio), la longitud máxima del muelle corresponderá a la longitud natural del muelle mas dos veces la amplitud de la oscilación:

Longitud máxima del muelle = L₀ + 2·A = 20 + 2·10 = 40 cm.

 

3. Al desplazar el cuerpo de la posición de equilibrio, ambas fuerzas seguirán actuando pero dejarán de estar equilibradas, por lo que podremos aplicar la 2ª ley de Newton para obtener la aceleración del movimiento

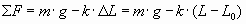
L representa la longitud del resorte en cualquier instante de la oscilación.

(Para poder establecer la comparación con el muelle oscilando en un plano horizontal, se toma como eje de oscilación el eje OY, y se considera sentido positivo hacia abajo y negativo hacia arriba)

Aplicando la igualdad que se da en la situación de equilibrio, vista en el apartado anterior:

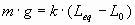
y sustituyendo en la expresión anterior

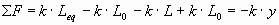
donde y = L - L_equlibrio

Así pues, si trasladamos el origen de coordenadas desde el extremo del muelle sin estirar a la posición de equilibrio cuando cuelga la masa, obtenemos una fuerza de tipo elástico que producirá el mismo M.A.S. que cuando se hace oscilar en posición horizontal (igual amplitud, frecuencia, velocidad,...), con la salvedad de que "y" ya no es el estiramiento del muelle respecto a su longitud natural, sino respecto a la nueva posición de equilibrio.

Así pues:

La amplitud de la oscilación será A = 10 cm = 0,1 m

La frecuencia de la oscilación será:

 

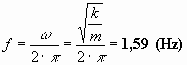
Y la velocidad cuando pase por la posición de equilibrio corresponderá a la velocidad máxima y será:
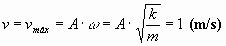