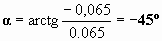Junio 03-04, Opción A

1. Escribe y comenta la Ley de Coulomb.

2. Las cuatro partículas de la figura están fijas en los vértices de un cuadrado de lado L = 30 cm. Sus cargas son q₁ = q₃ = 1 μ C y q₂ = q₄ = -1 μ C. Determina la fuerza eléctrica total (módulo, dirección y sentido) que actúa sobre q₁.

K = 1/4π ε₀ = 9·10⁹ N·m²·C^-2

1. La ley de Coulomb expresa matemáticamente la interacción electrostática, esto es la interacción entre cargas eléctricas en reposo.

Se enuncia: "La fuerza con la que interaccionan dos cargas eléctricas Q₁ y Q₂ separadas una distancia r es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia que las separa".

Matemáticamente:

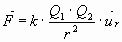
• u_r representa un vector unitario en la dirección de la recta que une ambas cargas y su sentido corresponde hacia una separación relativa de las cargas.

• Si las cargas son de distinto signo, la fuerza tendrá sentido negativo lo que significa que la fuerza será de atracción.

• Si las cargas son del mismo signo (positivas o negativas), la fuerza tendrá sentivo positivo lo que significa que la fuerza será de repulsión.

• La constante k (a diferencia de la constante de gravitación universal G) depende del medio en el que se encuentran las cargas, por esa razón se suele expresar en función de otra constante que es la permitividad o constante dieléctrica del medio, ε:

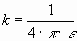
En el caso del vacío, el valor de k corresponde a 9·10⁹ N·m² /C²

Resumiendo:

• Varía con el inverso del cuadrado de la distancia, de forma similar a como varía la interacción gravitatoria

• Es una fuerza central y por lo tanto es conservativa.

• Su valor depende del medio en el que se encuentran las cargas.

• Puede ser atractiva o repulsiva (a diferencia del campo gravitatorio en el que únicamente existe la atracción)

2. Al ser la fuerza una magnitud vectorial (representamos los vectores en negrita y cursiva), resolvemos el ejercicio tomando como referencia los ejes cartesianos y los vectores directores unitarios i para el eje OX y j para el eje OY.

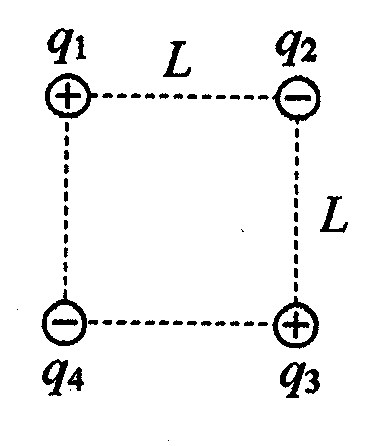
La fuerza total sobre la carga q₁ corresponderá a la suma vectorial de la fuerza que ejerce la carga q₂ sobre q₁ mas la fuerza que ejerce la carga q₃ sobre q₁ mas la fuerza que ejerce la carga q₄ sobre q₁.

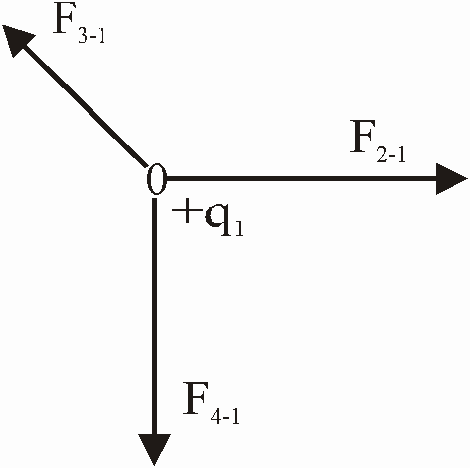
La expresión vectorial corresponde a:

F₁ = F_2-1 + F_3-1 + F_4-1

F₁ = F_2-1(+ i) + F_3-1 (- i + j)+ F_4-1 (- j)

F₁ = F_1x ( i ) + F_1y ( j ) = (F_2-1 - F_3-1(x))(+ i) + (F_3-1(y) - F_4-1)(j)

Calculamos por separado las componentes de la fuerza resultante:

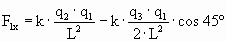
y

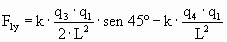
Sustituyendo los valores del enunciado, se obtiene:

F_1x = 0,065 N

F_1y = - 0,065 N

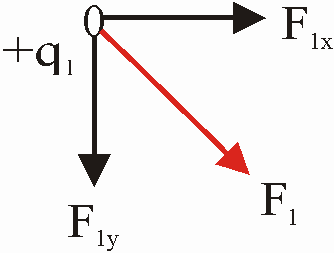
La expresión vectorial de la fuerza sobre la carga q₁ es:

F₁ = 0,065 ( i ) + 0,065 (- j )

El modulo será:

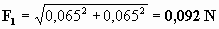
La dirección y sentido será: